Пример 1 ~ Пример 2 ~ Пример 3 ~ Пример 4 ~ Пример 5 ~ Пример 6 ~ Пример 7 ~ Пример 8

Пример 1. Найдем с помощью функции odesolve на отрезке [0, 4 p ] решение задачи Коши.

.

Решение примера в среде пакета Mathcad  
Вернуться на страницу <Mathcad-справочник. ОДУ>

Пример 2. Найдем с помощью функции odesolve на отрезке [0, 4 p ] решение граничной задачи

.

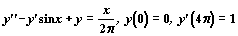Решение примера в среде пакета Mathcad
Вернуться на страницу <Mathcad-справочник. ОДУ>

Пример 3. Найдем на отрезке [0, p ] приближенное решение уравнения

y'=sin(xy),

удовлетворяющее начальным условиям y(0)=1 и построим график найденного решения.

Решим задачу численно, используя алгоритм Рунге-Кутты с фиксированным шагом на сетке из 20 равноотстоящих узлов.

Решение примера в среде пакета Mathcad
Вернуться на страницу <Mathcad-справочник. ОДУ>

Пример 4. Найдем на отрезке [0,3] приближенное решение уравнения

y''=exp(-xy),

удовлетворяющее начальным условиям

y(0)=1, y'(0)=1,

и построим график найденного решения.

Сведем решение задачи для уравнения второго порядка к задаче для эквивалентной нормальной системы второго порядка. Обозначим

y₁ =y(x), y₂ =y'(x);

поскольку y''(x)=(y'(x))'=y₂'(x) то получим

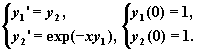
Решим задачу численно, используя алгоритм Рунге-Кутты с фиксированным шагом на сетке из20 равноотстоящих узлов.

Решение примера в среде пакета Mathcad
Вернуться на страницу <Mathcad-справочник. ОДУ>

Пример 5. Найдем на отрезке [0,3] приближенное решение задачи Коши

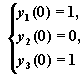
и построим графики для найденного решения.

Решим задачу численно, используя алгоритм Рунге-Кутты с фиксированным шагом на сетке из 20 равноотстоящих узлов.

Решение примера в среде пакета Mathcad
Вернуться на страницу <Mathcad-справочник. ОДУ>

Пример 6. Найдем на отрезке [0,2] приближенное решение задачи Коши

и построим графики найденного решения.

Эта система относится к классу жестких систем. Решим задачу численно на сетке из 20 равноотстоящих узлов с помощью функции Stiffr, предназначенной для решения жестких систем и использующей алгоритм Рунге—Кутты. Перед обращением к функции Stiffr необходимо, помимо начального вектора y и вектора правых частей D(x,y), определить матрицу J(x,y) размерности 2 x 3:

Решение примера в среде пакета Mathcad
Вернуться на страницу <Mathcad-справочник. ОДУ>

Пример 7. Построим фазовую и интегральную кривые решения задачи

найденного с помощью функции Stiffr (см. пример 6).

Решение примера в среде пакета Mathcad
Вернуться на страницу <Mathcad-справочник. ОДУ>

Пример 8. Построим векторное поле системы

.

Решение примера в среде пакета Mathcad
Вернуться на страницу <Mathcad-справочник. ОДУ>
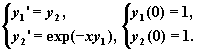
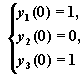