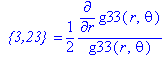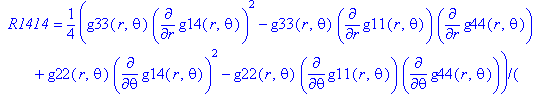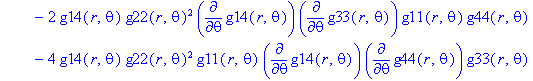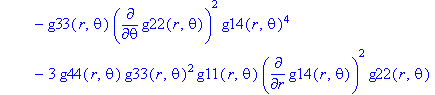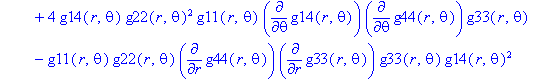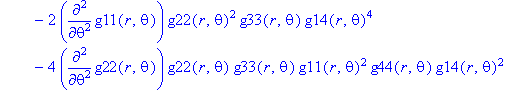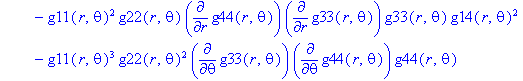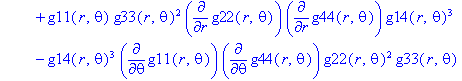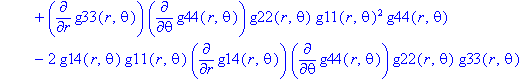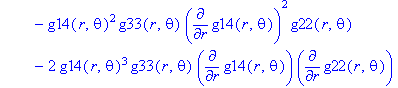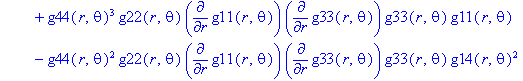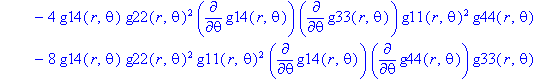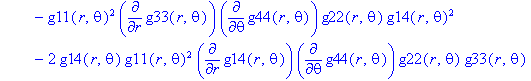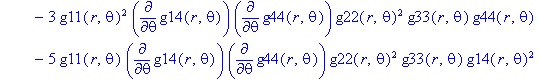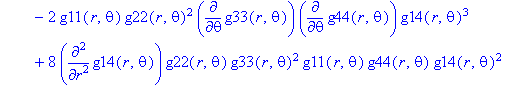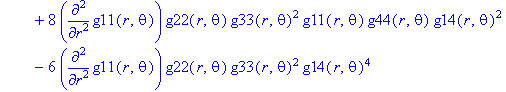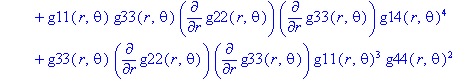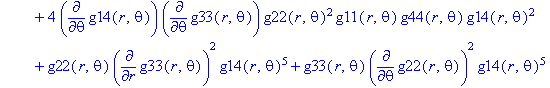Вернуться на страницу <Методические разработки>
В начало

1. Общий тензорный анализ в искривленном пространстве-времени с аксиальной симметрией

Обозначения

g - ковариантный метрический тензор, тензор второго ранга,

g_contr - контрвариантный метрический тензор, тензор второго ранга,

d1_g - ковариантная производная первого порядка от ковариантного метрическиого тензора, тензор третьего ранга,

d2_g - ковариантная производная второго порядка от ковариантного метрическиого тензора, тензор чевертого ранга,

Cf1 - символы Кристоффеля первого типа, "тензоры" третьего ранга,

Cf2 - символы Кристоффеля второго типа, "тензоры" третьего ранга,

Rm - ковариантный тензор Римана, тензор чевертого ранга,

Rc - ковариантный тензор Риччи, тензор второго ранга,

Rs - скаляр Риччи, тензор нулевого ранга,

Estn - тензор Эйнштейна, тензор второго ранга,

Weyl - ковариантный тензор Вейля, тензор чевертого ранга.

> with(tensor):

Сферические координаты

> coord := [t, r, theta, phi];

Компоненты ковариантного метрического тензора для аксиально-симметричного исривленного пространства-времени

> g := create([-1, -1], array(1..4, 1..4, symmetric, sparse,

[(1,1) = g11(r,theta), (2,2) = g22(r,theta), (3,3) = g33(r,theta),

(4,4) = g44(r,theta), (1,4) = g14(r,theta)]));

Компоненты контрвариантного метрического тензора для аксиально-симметричного исривленного пространства-времени

> `tensor/simp` := proc(a) simplify(a); end:

g_contr := invert(g, 'det_g');:

Ковариантная производная первого порядка от ковариантного метрическиого тензора

> d1_g := d1metric(g, coord):

Ковариантная производная второго порядка от ковариантного метрическиого тензора

> d2_g := d2metric(d1_g, coord):

Символы Кристоффеля первого типа

> Cf1 := Christoffel1(d1_g):

Символы Кристоффеля второго типа

> Cf2 := Christoffel2(g_contr, Cf1):

Компоненты тензора Римана

> Rm := Riemann(g_contr, d2_g, Cf1):

Компоненты тензора Риччи

> Rc := Ricci(g_contr, Rm):

Скаляр Риччи

> Rs := Ricciscalar(g_contr, Rc):

Компоненты тензора Эйнштейна

> Estn := Einstein(g, Rc, Rs):

Компоненты тензора Вейля

> Weyl := Weyl( g, Rm, Rc, Rs):

Ненулевые компоненты: символы Кристоффеля первого типа

> displayGR('Christoffel1', Cf1);

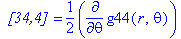
Ненулевые компоненты: символы Кристоффеля второго типа

> displayGR('Christoffel2', Cf2);

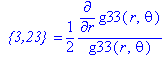
Ненулевые компоненты: тензор Римана

> displayGR('Riemann', Rm);

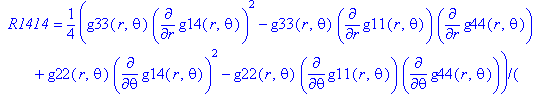
Ненулевые компоненты: тензор Риччи

> displayGR('Ricci', Rc);

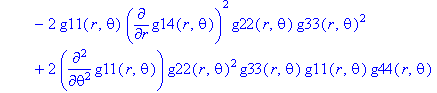
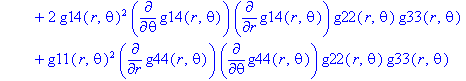
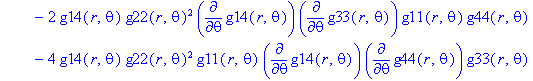
Скаляр Риччи

> displayGR('Ricciscalar', Rs);

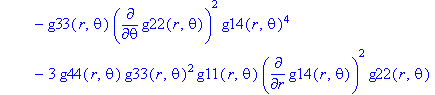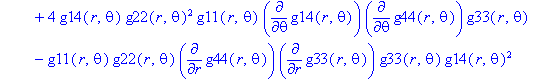
Ненулевые компоненты: тензор Эйнштейна

> displayGR('Einstein', Estn);

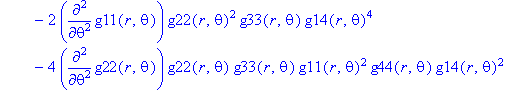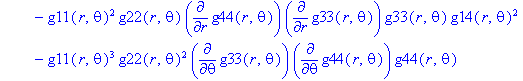
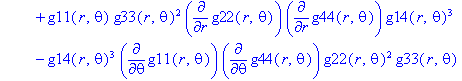
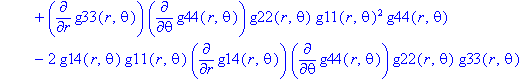
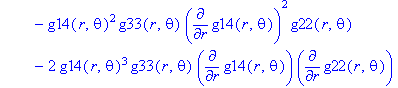
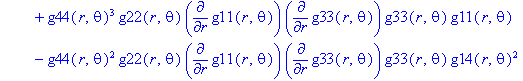
Ненулевые компоненты: тензор Вейля

> displayGR('Weyl', Weyl);

>

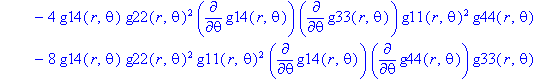
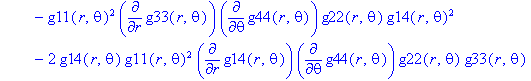
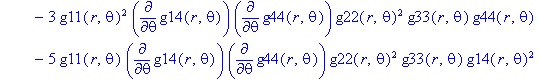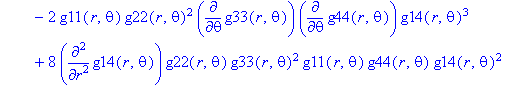
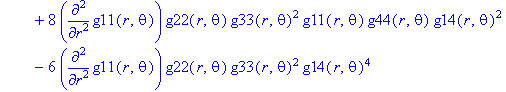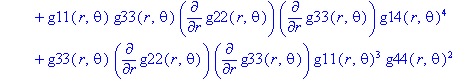
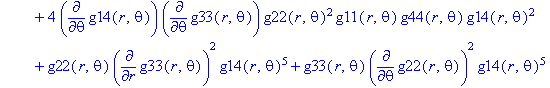
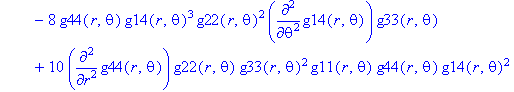
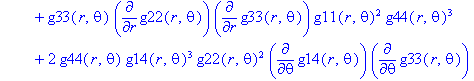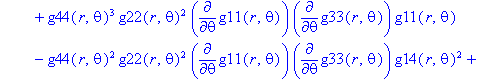
В начало
Вернуться на страницу <Методические разработки>